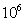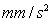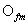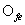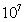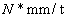魏然1, 王顯會1, 周云波1, 張明1
(1.南京理工大學 機械工程學院,江蘇 南京 210094)
摘 要:針對地雷爆炸環境下的某越野車車身底部結構,以降低整備質量、受沖擊載荷后的變形撓度、加速度、增加其底部結構的比吸能為目標響應,設置結構中各部件的厚度、幾何形狀為設計變量建立多目標優化模型。結合試驗設計和方差分析方法對設計變量進行參數篩選并建立優化模型的響應面;通過遺傳算法對響應面進行求解,得到了該優化問題的pareto解集,每個pareto解都是一個優化方案,可結合工程實際對pareto解集進行合理選擇,繼而指導該車輛底部結構設計;在pareto解集的基礎上使用標準邊界法得到了一個理想解,在盡量不增加結構質量的情況下,有效地提升了結構的防護性能。
關鍵詞:響應面法 多目標優化 參數篩選 標準邊界交叉法 爆炸防護
Multi-objective Optimization for Bottom Structure of Protective
Vehicle on Response Surface Methodology
Wei Ran1, Wang Xianhui1, Zhou Yunbo1, Zhang Ming1
(1.School of Mechanical Engineering, Nanjing University of Science & Technology,
Jiangsu Nanjing, 210094, China)
Abstract: The multi-objective optimization problem of vehicle bottom structure under landmine explosion is established by increasing complete vehicle kerb mass, deflection, acceleration and reducing specific energy absorption as response functions, besides the optimal design variables are consisted of the thickness and geometry parameters. A response surface is built by design of experiment and analysis of variance after parameter screening is completed. The multi-objective genetic algorithm is used to get the pareto solution set, every pareto solution is an optimal plan which could guide the design of vehicle bottom structure. Eventually, the normal-boundary intersection is applied to get an ideal solution which could give a comprehensive consideration of the contradiction between loss of weight and blast protection, the blast protection of structure is greatly promoted keeping up with the weight nearly unchanged.
Keyword: Response Surface Methodology, Multi-objective Optimization, Parameter Screening, Normal-boundary intersection, Protective vehicle
在反恐與維和任務中,對于軍用后勤車輛,來自反車輛地雷和簡易爆炸裝置IED(Improvised Explosive Device)的威脅與日俱增[1],為了提升乘員在車輛受到地雷襲擊時的生還率,現役軍車設計之初大多需要考慮其底部結構的抗爆炸沖擊特性[2]。越野車車身底部是受爆炸沖擊影響最大的車身構件之一,其防護性能直接關乎乘員的生存率,因此車身底部的抗爆炸沖擊性能是越野車車身結構優化的研究重點。隨著顯式動力學仿真分析的技術發展,地雷爆炸環境下車輛防護結構的響應仿真已成為可能,目前已有學者[3-5]對于軍用車輛的防護結構進行了小規模的仿真和優化研究。但由于整車的地雷爆炸仿真是一個高度非線性響應過程,其模型復雜、計算規模大(百萬級單元以上),很難通過仿真方法直接對車身進行參數篩選與結構優化。
解決上述問題可行的方法即結合試驗設計和數理統計,在不降低計算精度的前提下,構造計算快捷且能夠代替整車地雷爆炸有限元仿真的響應面,進而高效地對地雷爆炸環境下的車身結構進行優化。目前響應面法已被廣泛運用于工業界以解決碰撞、沖壓成型等非線性響應問題,如郝亮等[6]應用響應面對參數化的誘導槽吸能盒進行優化;丁煒琦等[7]通過響應面,對該客車結構的振動加速度、疲勞耐久性行了多目標優化;Honggang An[8] 在薄壁管件的沖壓成型仿真中的工藝設計建立響應面并對其進行了多目標的優化。
針對越野車車身底部結構的優化,首先通過試驗設計對車身底部結構設計變量篩選,然后以增加結構的比吸能,降低結構質量、受沖擊后的變形撓度、加速度為目標建立了響應面,最后通過多目標遺傳優化算法對響應面進行了優化,取得了理想的結果。
1 響應面法
在有限元的結構優化問題中使用響應面可大大縮短優化迭代的計算時間、減少工程師因重復建模帶來的工作量,同時也可以避免優化中形狀變量交叉變化造成的有限元模型網格質量下降導致計算結果不收斂的情況。其基本思想是通過試驗設計進行設計樣本空間,最后通過曲線擬合的方法建立響應面。
1.1 試驗設計
試驗設計是一種對試驗進行合理安排的數理統計方法,并以較小的試驗周期、試驗成本獲得理想的試驗結果。比較常見的試驗設計方法有中心復合試驗、拉丁超立方試驗、哈摩斯雷試驗設計等。
在建立越野車車身底部結構優化響應面中,由于單次的整車爆炸仿真試驗耗時較長,試驗設計中應盡量縮減試驗中水平值。推薦使用plack-burman試驗建立參數篩選的樣本空間,plackett-burman試驗是一種多變量2水平的篩選試驗,各個變量的水平差值不能過大(高水平為低水平的1.5倍以內),不考慮因子之間的交互效應,通過plackett-burman采樣結合方差分析(analysis of variance, ANOVA)能高效地對多因子空間的結構變量進行一階靈敏度分析,從而有效地判斷個變量對響應函數的貢獻,縮減變量的樣本空間;在對其優化數學模型進行曲線擬合的樣本空間建立中,考慮變量之間的主效應、交互作用外、二次效應變得必要,故推薦使用正交中心復合試驗[9](Orthogonal-Composite Design of Experiment,CCD)設計。
1.2 響應面法理論
是數學與數理統計相結合的一種全局近似模型的方法,對于高度非線性動力響應問題具有顯著優勢。響應面法可以將復雜的難以表達為顯式函數關系的目標函數和約束條件表示為簡單的顯式函數,為后續的分析、優化等工作提供良好基礎。在完成了試驗設計的樣本采樣之后,根據不同類型的目標響應函數,利用最小二乘法或者移動最小二乘法[10](Moving Least Square)進行曲線擬合,從而構建響應面。其基本思想是設目標響應函數與設計變量之間的關系滿足如下線性方程組:
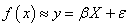 (1)
(1)
式中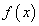 為目標響應函數,
為目標響應函數,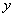 為擬合曲線函數,
為擬合曲線函數,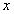 為設計變量,
為設計變量,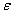 為擬合誤差,一階、二階響應面多項式展開表示為:
為擬合誤差,一階、二階響應面多項式展開表示為:
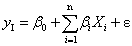 (2)
(2)
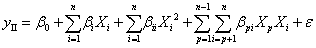 (3)
(3)
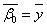 ;
; 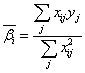
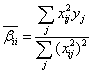 ;
; 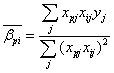 (4)
(4)
式中,n為變量的個數,i、j、p為臨時變量,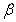 為通過最小二乘法得到的響應面回歸系數。為了說明y與f(x)之間的擬合精度,引入pearson相關系數[11]:
為通過最小二乘法得到的響應面回歸系數。為了說明y與f(x)之間的擬合精度,引入pearson相關系數[11]:
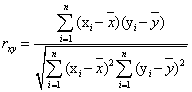 (5)
(5)
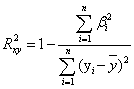 (6)
(6)
式中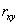 、
、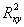 定義域為(0,1),person系數越接近1,說明變量與擬合函數之間的相關性越高。當離散的響應值分布廣、形狀復雜時,使用最小二乘法得到的線性方程組往往不能很好的擬合出響應面(相關系數不接近1),在不增加試驗樣本空間的情況下,可采用移動最小二乘法來擬合響應面,其基本思想近似與最小二乘法,只是將擬合區域分為數個子區域,各個區域內的分段響應函數只與該子區域內的變量進行擬合,由此移動最小二乘法擬合得到的響應面雖然不能以線性方程組的形式表示,卻可在樣本空間不足的情況下高精度地擬合響應面,其表達式如下:
定義域為(0,1),person系數越接近1,說明變量與擬合函數之間的相關性越高。當離散的響應值分布廣、形狀復雜時,使用最小二乘法得到的線性方程組往往不能很好的擬合出響應面(相關系數不接近1),在不增加試驗樣本空間的情況下,可采用移動最小二乘法來擬合響應面,其基本思想近似與最小二乘法,只是將擬合區域分為數個子區域,各個區域內的分段響應函數只與該子區域內的變量進行擬合,由此移動最小二乘法擬合得到的響應面雖然不能以線性方程組的形式表示,卻可在樣本空間不足的情況下高精度地擬合響應面,其表達式如下:
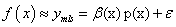 (7)
(7)
式中,設計變量基函數為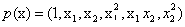 ,
,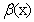 為回歸系數函數,
為回歸系數函數,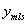 為移動最小二乘法得到的擬合函數。
為移動最小二乘法得到的擬合函數。
1.3 響應面建立流程
越野車車身底部結構優化問題包含的設計變量、目標響應函數鉸多,建立其響應面步驟如下(參考圖1):
(1)車身底部爆炸仿真模型標定后,初步確定結構的設計變量和目標響應;
(2)使用試驗設計(plack-burman試驗)建立篩選試驗;
(3)通過方差分析對篩選試驗結果進行一階靈敏度分析,縮減設計變量空間,確定優化數學模型;
(4)對新的變量空間使用試驗設計(CCD)建立樣本空間;
(5)使用曲線擬合(最小二乘法或移動最小二乘法)建立響應面。
(6)進行相關性檢驗
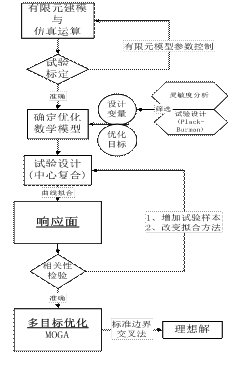
圖1 基于響應面的結構多目標優化流程
2 多目標遺傳優化
越野車車身底部結構優化是一個多目標優化問題,各個目標響應函數之間存在沖突,例如為了降低質量,需要縮小防護板厚,而為了增加防護又需要增加板厚,因此這類優化問題往往無法得到一個最優解。故首先引入經典的多目標遺傳算法[12](Multiobjective Optimization Genetic Algorithms,MOGA)求出響應面的pareto解集,再利用標準邊界交叉法[13](Normal-boundary intersection,NBI)得到了在pareto解集中的一個理想解。
2.1 多目標遺傳算法
不同于傳統的多目標問題將多個目標考慮為獨立的子問題,通過先決策后尋優的思想,利用線性加權的辦法得到一個最優解,MOGA是一種在pareto占優法的基礎上得到不劣解集的多目標優化方法,此算法借用了生物遺傳學的觀點,通過自然選擇、遺傳、變異等作用機制,主要通過交叉、變異、選擇運算實現。交叉或變異運算不斷迭代,使可行域中的變量朝著最優的方向移動,變量通過遺傳算子的作用以啟發式的進化搜索生成下一代的變量,再通過適應度函數來評價變量的優劣。所有的pareto集都是可行的優化方案,一般求最小值的多目標問題表達式如下:
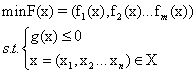 (8)
(8)
式中F為目標響應函數向量,m為目標響應函數的個數,g為約束函數,X為變量的定義域,n為變量系數。在結構優化問題中,Pareto法的數學定義為:任意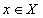 ,不存在
,不存在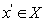 使得
使得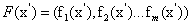 占優于
占優于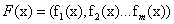 ,
,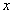 即為X上的pareto最優解,其中
即為X上的pareto最優解,其中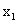 占優于
占優于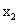 指
指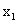 的所有目標函數都小于
的所有目標函數都小于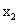 。以最簡單的雙目標優化問題為例(圖2),在可行解空間中
。以最簡單的雙目標優化問題為例(圖2),在可行解空間中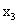 占優于
占優于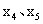 ;
;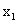 與
與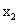 占優于
占優于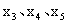 ,故pareto最優前沿由
,故pareto最優前沿由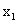 與
與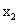 決定,因此MOGA通過迭代所得到的滿意解集將集中在pareto最優前沿曲線(圖2中粗實線)附近,在
決定,因此MOGA通過迭代所得到的滿意解集將集中在pareto最優前沿曲線(圖2中粗實線)附近,在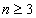 的情況中,pareto最優前沿變為一個空間曲面。
的情況中,pareto最優前沿變為一個空間曲面。
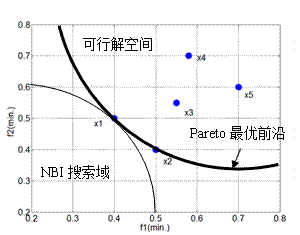
圖2 多目標遺傳優化方法
2.2 標準邊界交叉法
標準邊界交叉法由Das I[14]開發,NBI及其衍生算法優點是適用性強,可計算n維空間多目標優化問題(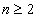 ),算法簡單、高效。對于求理想解的最小化問題基本思想是:
),算法簡單、高效。對于求理想解的最小化問題基本思想是:
(1)將目標響應函數F(x)所得到的最優pareto最優前沿進行去量綱的標準化:
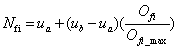 (8)
(8)
式中,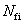 為標準化之后的第i個響應函數,
為標準化之后的第i個響應函數,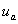 、
、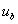 分別是坐標軸邊界的上、下限,
分別是坐標軸邊界的上、下限,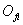 是通過MOGA得到的第i個pareto解,
是通過MOGA得到的第i個pareto解,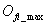 是pareto解集的中最大值。通過合理地搭配
是pareto解集的中最大值。通過合理地搭配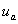 、
、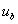 的值可以使得標準化之后的pareto前沿上的解更集中。
的值可以使得標準化之后的pareto前沿上的解更集中。
(2)通過NBI搜索域(圖2)找出其pareto最優前沿上的理想解,搜索半徑公式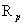 為:
為:
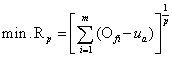 (9)
(9)
式中,m為目標函數的個數,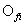 為第
為第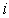 個目標函數的最優解集,P可取
個目標函數的最優解集,P可取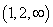 ,在算例中取p=2。
,在算例中取p=2。
3 某越野車車身底部優化算例
由于某防護型車身具有一定的對稱性,使用pro/E、hyperworks對三維模型進行必要的幾何清理、模型簡化,對模型各個零部件進行網格劃分,并檢查單元質量,對整車有限元模型進行裝配。使用LS-DYNA對其1/2模型進行地雷爆炸仿真分析,在眾多的爆炸仿真算法中,選擇目前穩定性與精度較佳的多物質單元流-固耦合法[16](Arbitrary Lagrange—Eulerian,ALE),空氣單元網格需要覆蓋整個防護型車倆的底部結構,模型(包括空氣、地雷替代物單元)單元總數為1112746,節點總數為1148829,單位選用噸-mm-s。
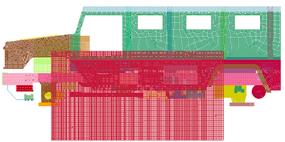
圖3 車身與空氣有限元模型
模擬的時間為地雷起爆后的8ms,在地雷爆炸0.2ms后沖擊波接觸V形底板,3ms之后離開駕駛室底部,如圖4節點位移(單位mm)云圖所示,該車輛底部結構在極短時間受到爆炸沖擊波襲擊后產生塑形變形,駕駛室底板也因此受到較大影響,故有必要對該車輛底部結構進行優化設計。
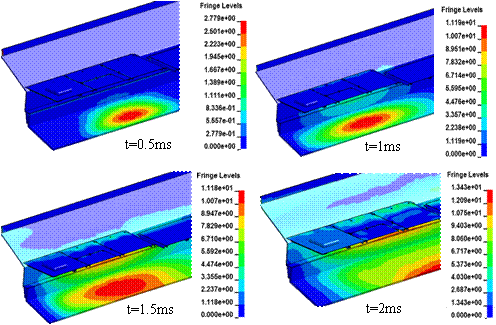
圖4 車輛底部1/2模型爆炸仿真位移云圖
3.1 確定優化數學模型
該車輛底部優化的目標是提升其結構的抗爆炸沖擊性能,為了定量地分析車輛底部結構的抗爆炸沖擊性能,首先要確定其優化數學模型。如圖5所示,在該算例中通過駕駛室底板(駕駛員腳部位置)構件的加速度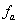 、底部V形板在爆炸沖擊波下的變形撓度
、底部V形板在爆炸沖擊波下的變形撓度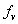 、車身底部結構的比吸能
、車身底部結構的比吸能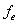 為目標函數進行評價,同時由于加裝甲所增加的質量必然會影響其整車性能[15],因此在優化目標函數中還考慮了整車質量
為目標函數進行評價,同時由于加裝甲所增加的質量必然會影響其整車性能[15],因此在優化目標函數中還考慮了整車質量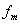 。
。
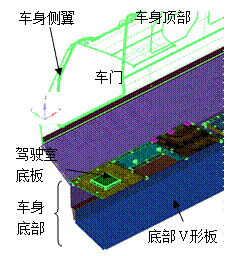
圖5 某越野車車身1/2有限元模型
該車輛底部結構主要由底部的側板、V形側板、V形底板(對應圖6中的板1,初始厚度10mm;板2,初始厚度10mm、板3,初始厚度16mm)構成。在該算例中需要考慮各個結構板的厚度和形狀,因此設計變量包括5個形狀變量(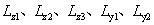 )和3個尺寸變量(
)和3個尺寸變量(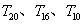 )。故通過公式(8),該算例的優化數學模型可表示為:
)。故通過公式(8),該算例的優化數學模型可表示為:
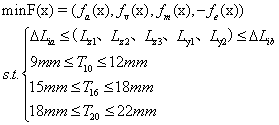 (10)
(10)
式中,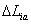 、
、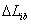 分別為各個類型變量的上下邊界,由于底部結構的比吸能
分別為各個類型變量的上下邊界,由于底部結構的比吸能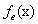 是目標函數的最大值,故在
是目標函數的最大值,故在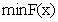 中取負值。
中取負值。
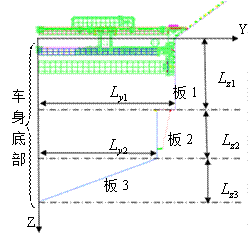
圖6 底部結構設計變量示意圖
3.2 參數篩選與響應面建立
根據初步確定的數學優化模型,利用plack-burman試驗的采樣,建立因子數為8,水平數為2的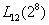 的參數篩選試驗,結合ANVOA方法分別對4個響應函數
的參數篩選試驗,結合ANVOA方法分別對4個響應函數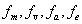 計算處8個變量
計算處8個變量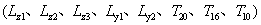 的貢獻率(參考圖6):
的貢獻率(參考圖6):
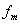 質量影響:
質量影響: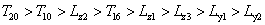 ;
;
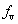 撓度影響:
撓度影響: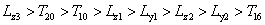 ;
;
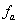 加速度影響:
加速度影響: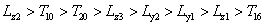 ;
;
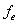 比吸能影響:
比吸能影響: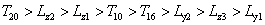 。
。
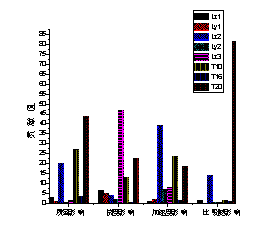
圖7 設計變量貢獻率
為了縮減樣本空間,排除對4個響應函數貢獻較小的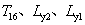 ,在后續的優化中將這3個變量設為等于初始值的常數。在新的變量空間考慮變量之間的交互性,建立因子數為5,水平數為5的正交中心復合試驗
,在后續的優化中將這3個變量設為等于初始值的常數。在新的變量空間考慮變量之間的交互性,建立因子數為5,水平數為5的正交中心復合試驗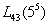 ,結合公式(1—4)、(7),可得到相應函數的二次多項式方程組(加速度響應使用移動最小二乘法),進而得到4個目標函數的響應面。(以二次多項式方程組的形式描述):
,結合公式(1—4)、(7),可得到相應函數的二次多項式方程組(加速度響應使用移動最小二乘法),進而得到4個目標函數的響應面。(以二次多項式方程組的形式描述):
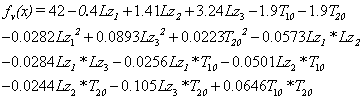
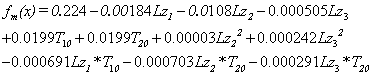
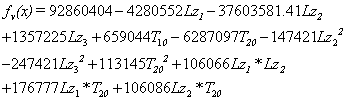 (11)
(11)
由于直接使用最小二乘法對目標函數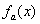 精度較差,利用移動最小二乘法可得到
精度較差,利用移動最小二乘法可得到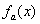 的響應面(以空間曲面的形式描述):
的響應面(以空間曲面的形式描述):
|
|
|
|
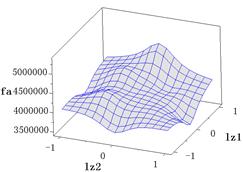
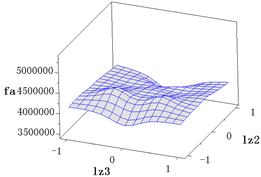
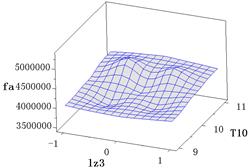
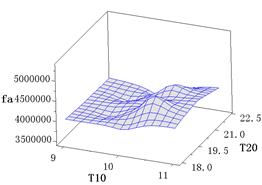
圖8 目標函數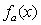 響應面
響應面
根據公式(5)、(6)繼而得到響應面的相關系數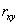 、
、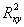 (參考表1,
(參考表1,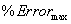 是響應面與仿真試驗的最大相對誤差)。
是響應面與仿真試驗的最大相對誤差)。
表1 響應面精度
響應 函數 |
|
|
|
| 0.987 | 0.984 | 0.6 |
| 0.982 | 0.924 | 1.6 |
| x | x | 3.7 |
| 0.942 | 0.938 | 3.3 |
3.3 優化及結果分析
在得到準確的響應面基礎上利用MOGA算法對響應函數進行優化,設置pareto解個數為500,遺傳代數為50代,每代精英數量為樣本空間的10%,變異率為0.01。計算得到的pareto最優空間解集(圖9,pareto最優前沿曲面在2個不同響應函數為坐標的投影),所有的pareto解集(共500個,藍色點云)均代表該車輛底部結構優化的解,在防護車輛的設計中,可根據工程實際在pareto解集中進行人工選擇。
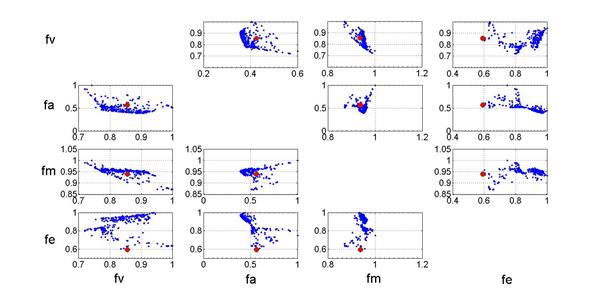
圖9 pareto最優解集及理想解
在得到pareto空間最優解集的基礎上,繼續使用NBI找出理想解,在公式(8)基礎上對響應函數進行標準化,為了使得解集在空間上更加集中,標準化公式如下:
 (12)
(12)
式中,由于比吸能響應函數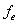 需要求出其最大值,
需要求出其最大值,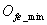 是其pareto解集的中最小值。最后利用公式(9)可在500組pareto解空間中找出
是其pareto解集的中最小值。最后利用公式(9)可在500組pareto解空間中找出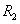 最小的值(圖8中紅色點,第52組參考表2),即為該算例的理想值。
最小的值(圖8中紅色點,第52組參考表2),即為該算例的理想值。
表2 部分pareto解及標準化后的pareto解
序號 |
(mm) |
( |
(t) |
( |
|
|
|
|
| |||||
0 | 7.439 | 4.320 | 0.938 | 1.569 | ||||||||||
1 | 6.550 | 2.121 | 0.962 | 1.080 | 0.830 | 0.422 | 0.954 | 0.948 | 1.636 | |||||
… | ||||||||||||||
51 | 6.983 | 1.895 | 0.962 | 1.061 | 0.875 | 0.403 | 0.954 | 0.964 | 1.663 | |||||
52 | 6.815 | 3.492 | 0.943 | 2.107 | 0.862 | 0.578 | 0.939 | 0.595 | 1.517 | |||||
53 | 6.736 | 2.678 | 0.974 | 1.173 | 0.858 | 0.483 | 0.965 | 0.897 | 1.634 | |||||
… | ||||||||||||||
500 | 8.128 | 3.442 | 0.865 | 1.870 | 0.982 | 0.560 | 0.878 | 0.632 | 1.565 | |||||
表2中,第0組數據由優化前該車輛的原始參數計算得到,通過比較可知,最終的理想解在結構質量基本不變的情況下(增加了0.6%,共6kg),底部變形撓度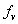 縮小了7.2%、駕駛室底板加速度
縮小了7.2%、駕駛室底板加速度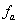 縮小了19.2%、底部結構比吸能
縮小了19.2%、底部結構比吸能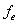 增加了34.3%。
增加了34.3%。
4 結 論
(1)結合響應面法和多目標遺傳算法能準確高效地解決該越野車車身底部結構優化問題,采用流程式的程序思想提高了設計人員效率、節省了計算資源,該方法與理論也適用于其他的結構優化問題。
(2)通過一階靈敏度分析對優化模型的眾多設計變量進行了參數篩選,說明在該車輛底部結構V形側板的厚度、底部結構水平截距對其響應函數的貢獻較小;V形底板的厚度、幾何參數對改善其防護性能作用較大。
(3)通過多目標遺傳算法得到的pareto解集具有重要參考意義,每個解都是一個優化方案,可結合工程實際對pareto解集進行合理選擇,繼而指導該車輛底部結構設計。
(4)通過標準邊界交叉法能高效處理多目標優化問題,得到的理想解也表明該算法可綜合考慮防護性能和質量的矛盾關系,在盡量不增加結構質量的情況下,最大幅度地提升其防護性能。
參考文獻
[1] M Grujicic, G Arakere, H Nallagatla, W C Bell . Computational investigation of blast survivability and off-road performance of an up-armoured high-mobility-multi-purpose wheeled vehicle. Automobile Engineering[J]. 2009:301-303.
[2] 韓守紅,呂振華.軍車駕駛室結構抗爆炸特性的數值仿真[C].//第十屆全國沖擊動力學討論會論文集.2011:1-9.
[3] Jiulong Sun , Nickolas Vlahopoulos, Tara J. Stabryla and Rich Goetz .Blast Event Simulation for a Structure Subjected to a Landmine Explosion[J]. SAE International, 2006-01-0931.
[4] 董彥鵬,呂振華. 基于蜂窩材料結構相似有限元模型的夾層結構抗爆炸沖擊特性優化設計分析[J]. 工程力學,2013,07:248-254.
[5] 王飛,陳衛東.爆炸沖擊載荷作用下板殼結構數值仿真分析[J].強度與環境.2010,8,37(4):37-39.
[6] 郝亮,徐濤,崔健,吉野辰萌. 參數化誘導槽設計的吸能盒結構抗撞性多目標優化[J]. 吉林大學學報(工學版),2013,01:39-44.
[7] 丁煒琦,田程,范子杰. 基于代理模型的大客車結構動態特性多目標優化[J]. 汽車工程,2012,12:1072-1075+1093.
[8] Honggang An, Daniel E. Green, Jennifer Johrendt. Multi-objective optimization and sensitivity analysis of tube hydroforming. Int J Adv Manuf Technol (2010) 50:67–84.
[9] Nuran Bradley. The response surface methodology [D]. South Bend: Department of Mathematical Sciences ,Indiana University of South Bend,2007.
[10] 張勇,李光耀,鐘志華. 基于移動最小二乘響應面方法的整車輕量化設計優化[J]. 機械工程學報,2008,11:192-196.
[11] I.M. Sobol. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Mathematics and Computers in Simulation 55 (2001) 271–280.
[12] Honggang An, Daniel E. Green, Jennifer Johrendt. A hybrid-constrained MOGA and local search methodto optimize the load path for tube hydroforming. Int J Adv Manuf Technol (2012) 60:1017–1030.
[13] Rigoni E (2004) NBI-NLPQLP Scheduler, Technical Report2004-003.
[14] Das I, Dennis JE (1998) Normal-boundary intersection: a new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM J Optim 8(3):631–657.
[15] M. Grujicic, H. Marvi, G. Arakere, W.C. Bell and I. Haque. The effect of up-armoring of the high-mobility multi-purpose wheeled vehicle (HMMWV) on the off-road vehicle performance. Multidiscipline Modeling in Materials and Structures Vol. 6 No. 2, 2010 pp. 229-256.
[16] 李利莎,謝清糧,鄭全平,張洪海.基于Lagrange, ALE和SPH算法的接觸爆炸模擬計算[J].爆破,2011,28(1).