趙春來,臧孟炎
(華南理工大學機械與汽車工程學院 廣州)
摘 要:采用離散元與有限元耦合方法(FEM/DEM)模擬輪胎沙石路面相互作用,提出 “路面更替法”,以控制仿真模型規模,提高計算效率。建立剛性有限元輪胎在離散元沙石路面上行駛的三維仿真模型,使用自主開發軟件CDFP對剛性車輪砂石路面行駛行為進行仿真分析。獲取了輪胎掛鉤牽引力、下陷量、沙石顆粒流動趨勢等行駛行為參數。通過與相關實驗結果對比,驗證了該方法的可行性。
關鍵詞:越野車輛;通過性能;沙石路面;FEM/DEM;路面更替
中圖分類號:U461.5+1 文獻標志碼:A
深入研究輪胎-沙粒間的相互作用對高水平越野車的設計、性能評價等具有重要的指導意義。然而,單純使用有限元方法(FEM)雖然能夠很好地描述輪胎特性[1-5](包括輪胎的復雜花紋形狀、充氣輪胎的變形等),但在研究越野車輛沙地行駛行為評價方面遇到了挑戰:由于沙石路面具有典型的非連續介質特性,用傳統的連續介質理論(如:FEM)不能合理描述其運動行為。離散元方法(DEM)在描述散體介質的非連續特性方面具有明顯優勢[6-9]。
為了兼顧FEM和DEM的優點,Nakashima[10-12]等采用二維離散元與有限元耦合方法(FEM/DEM)研究輪胎在沙石路面上的行駛行為,并開發了相應的計算程序。但是,二維方法在研究輪胎行駛行為時存在很多局限性,例如:無法描述輪胎花紋、沙石顆粒的側向流動及輪胎側向力等。本文介紹了一種我們自主開發的、適用于越野車輪胎行駛行為仿真分析的三維FEM/DEM計算方法,然后針對越野車輛沙地行駛過程的特點,提出了“路面更替法”以控制仿真模型規模,并基于FORTRAN 95語言開發了相應的專用分析軟件。
1 方法介紹
1.1 FEM/DEM算法介紹
本文所述FEM/DEM方法在車輪-沙地相互作用分析的本質是使用FEM來模擬輪胎,用DEM方法來描述沙粒。離散單元及與沙石接觸輪胎有限單元節點的運動受牛頓第二定律控制。算法中包含圖1(a)、(b)所示的兩種接觸類型:(1)離散單元間的接觸;(2)離散單元與有限單元間的接觸。這兩種接觸類型分別用來描述沙石顆粒間的相互作用和輪胎與沙石顆粒間的相互作用。其中前者采用Williams等提出的‘C-grid’方法[13]進行接觸判斷,后者采用作者開發的適用于球形離散單元和六面體有限單元的NTS算法[14]。
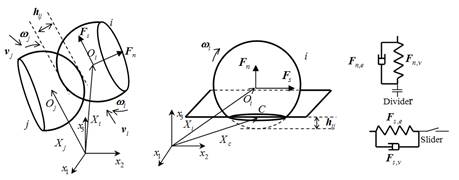
(a) 離散單元間相互作用 (b) 離散元與有限元相互作用 (c) 單元間作用力
圖1 單元接觸模型
圖1中,hij為單元間的重疊量,vi、vj、ωi、ωj分別為單元i和j的速度和角速度。Fn和Fs分別為單元間的法向力和切向力,如式(1)、(2)所示,其中切向力Fs滿足庫倫摩擦定律。
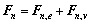 (1)
(1)

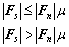 (2)
(2)
式中,Fn,e、Fn,v、Fs,e、Fs,v分別為單元間的法向彈簧力、法向阻尼力、切向彈簧力和切向阻尼力,通過Hertz-Mindlin理論求解[15]。μ為單元間的摩擦系數。求解有限單元與離散單元間作用力時,將有限單元視為半徑無窮大的離散單元[16]。
輪胎與沙石顆粒相互作用的二維示意圖如圖2所示,車輪用有限元描述,沙石路面用離散元描述。輪胎沿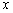 正方向行駛。輪胎的掛鉤牽引力N、輪胎所受的路面豎直方向反作用力P及輪胎滑轉率s分別為
正方向行駛。輪胎的掛鉤牽引力N、輪胎所受的路面豎直方向反作用力P及輪胎滑轉率s分別為
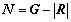 (3)
(3)
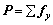 (4)
(4)
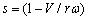 (5)
(5)
其中,G=Σfx+;R=Σfx-;f為輪胎與沙石顆粒間的相互作用力;V為輪胎質心水平速度; r為輪胎的滾動半徑,對剛性輪胎,滾動半徑等于輪胎自然半徑;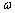 為輪胎的角速度。
為輪胎的角速度。
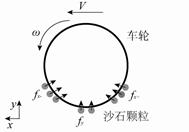
圖2 輪胎與路面間的相互作用示意圖
2.2 路面置換法
離散元方法在描述非連續的沙石路面時具有優勢,但該法計算效率較低,而影響計算效率的主要因素是參與計算的離散單元的數量。實際當中,車輪后方一定范圍外,被碾壓過的沙石顆粒對車輪行駛行為的影響可以忽略,同時,車輪前方一定距范圍外,沙石顆粒對車輪行駛行為影響也較小。基于此,我們提出一種“路面更替法”,以控制參與計算的離散單元數目,提高計算效率。下面通過二維示意圖描述該方法的主要步驟:
(1)首先,在給定區域內生成離散單元集,作為初始沙石路面樣本,記為DES A0,長度為a,如圖3(a)所示;
(2)第二,將上一步中的離散單元集DES A0復制兩份,分別記為DES A1和DES A2,并按順序排列,組成長度為2a的初始路面,如圖3(b)所示;
(3)第三,將車輪放置在路面DES A1中間位置,車輪在自重及外載荷作用下自由下沉,直到輪胎所受的路面法向反作用力等于車輪自重及外載荷之和。然后給車輪施加恒定的角速度和相應的水平速度,使車輪在某一滑轉率下行駛,如圖3(c)所示;
(4)第四,當車輪行駛到DES A2的中間位置時,DES A1對車輪行駛行為影響可以忽略,且DES A2前端沒有發生明顯破壞,此時開始進行第一次路面更替:將DES A1刪除,同時重新備份路面樣本,記為DES A3,放置在DES A2前端,與DES A2組成新的路面,如圖3(d)所示。
反復執行步驟(4),參與計算的沙石路面長度始終等于2a,可以實現較少數量的離散單元來模擬任意長度的沙石路面,大幅提高計算效率的目的。對于由多種結構路面構成的越野車輛沙地通過性能評價,只需對每種結構路面生成樣本路面,然后根據車輪即將行駛的路面結構調入對應結構樣本路面即可。

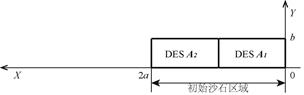
(a) 沙石區域樣本 (b) 組成初始沙石區域
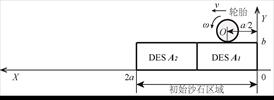

(c) 放置輪胎 (d) 路面更替
圖3 路面置換方法的二維示意圖
同種路面結構相應的程序流程圖如圖4所示,其中Tter為計算終止時間,Δt為顯式算法的時間步長,T為當前計算時間。
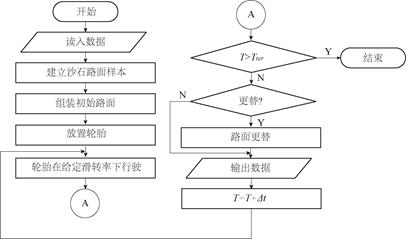
圖4 執行流程圖
3 數值算例
為驗證方法的有效性,基于室內土槽實驗[17],建立了輪胎在沙石路面行駛的三維仿真模型,分析了不同滑轉率下輪胎的行駛行為。
3.1 離散元沙石路面
首先,采用作者之前開發的分層生成方法[18],在指定區域內,隨機生成給定半徑范圍的球形離散單元集,區域邊界采用剛性墻約束。然后,讓初始生成的離散單元在自重作用下達到穩定狀態,以模擬自然沙地。最終生成的離散元在X: (0,735)、Y: (0,480)、Z: (0,280)范圍,離散單元集孔隙率約為0.32,以此作為沙石路面初始樣本,如圖5所示。本文側重于對開發方法的驗證,因此,離散單元半徑范圍取6~7mm,大于實際沙粒半徑。自重壓實過程離散單元總勢能的時間歷程如圖6所示,在1.1s以后,其趨勢基本平穩,此時可以認為壓實過程結束。
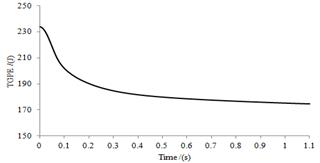
圖5 初始沙石路面樣本 圖6 離散元沙石顆粒重力勢能時間歷程
楊氏模量:75000 MPa,泊松比:0.3,密度:2400 kg/m3,單元數目:45551,摩擦系數:0.3
3.2 初始路面及車輪模型
初始沙石路面區域由兩段經自重壓實后的“路面樣本”組成,單元總數為91102個,長度等于路面樣本長度二倍的1470mm。有限元車輪采用如圖7所示的簡化模型,暫不考慮輪胎變形。輪胎與沙路間的摩擦系數為0.4,輪胎放置在如圖所示位置。給輪胎施加自重及外載荷(計1295N)同時加載恒定的角速度0.5rad/s和相應的水平速度,使輪胎在給定滑轉率下沿X軸正方向行駛。
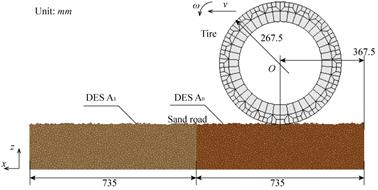
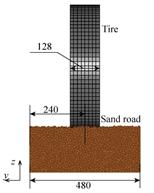
(a) 主視圖 (b) 左視圖
圖7 初始路面和有限元輪胎模型
輪胎參數:楊氏模量:2 MPa,泊松比:0.49,密度:1800 kg/m3,單元數目:1344
3.3 仿真結果
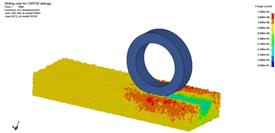
當車輪行駛距離為k×735 mm(k為路面更替次數)時執行路面更替。圖8給出輪胎在30%滑轉率下,離散單元Z方向的位移云圖:圖8(a)為初始狀態;圖8(b)為輪胎行駛到第二段樣本路面中間位置時的車轍;圖(c)為執行第一次沙石路面更替后的車轍;圖8(d)給出了第二路面更替前的車轍狀況;圖8(e)執行了第二次路面更替;圖8(f)為計算終止狀態,車輪行駛距離為1560mm。

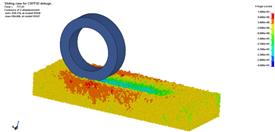
(a) (b)
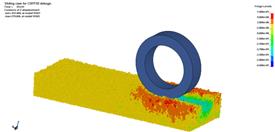
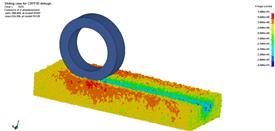
(c) (d)
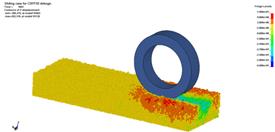
(e) (f)
圖8 車輪滑轉率為30%時沙石顆粒Z方向位移云圖
圖9為輪胎在滑轉率為30%時的輪胎掛鉤牽引力時間歷程。掛鉤牽引力在初始階段有一個較大峰值,主要原因是初始階段,輪胎與路面間豎直方向有相對沖擊速度,產生一個沖擊力,引起路面法向反作用力出現峰值,與此相應,掛鉤牽引力初始階段也出現峰值。隨后掛鉤牽引力快速減小,但仍有較大波動,主要原因是離散單元顆粒半徑取值較大,對接觸力計算結果影響所致。
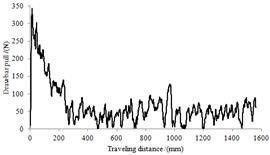
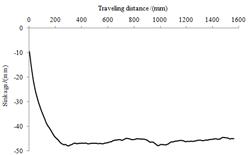
圖9 滑轉率為30%時車輪行駛過程 圖10 滑轉率為30%時車輪行駛過程中的
中的輪胎掛鉤牽引力時間歷程 輪胎下陷量時間歷程
圖10為輪胎行駛過程中的下陷量時間歷程,由圖可知:在初始階段,輪胎下陷量快速增加,主要原因是輪胎豎直方向載荷未達到平衡狀態。在行駛200mm之后,下陷量基本上趨于一個穩定的狀態,均值約為45mm,且在路面更替時未出現明顯波動。
圖11為輪胎在30%滑轉率下行駛時,沙石顆粒的流動趨勢,圖中箭頭表示離散單元在X-Z平面內的速度矢量。由圖可知:沙石顆粒的流動趨勢可分為兩個區域:前區,繞順時針方向;后區,繞逆時針方向。該現象與莊繼德[19]等人的實驗研究結果基本一致。
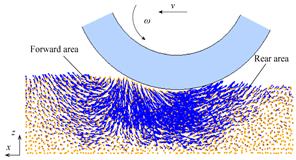
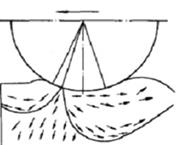
(a) 仿真結果 (b) 實驗結果
圖11 車輪行駛過程中沙石顆粒的運動趨勢
滑轉率是影響輪胎行駛行為的主要因素,為研究不同滑轉率下輪胎的行駛行為,圖12和圖13分別給出了輪胎下陷量和掛鉤牽引力隨滑轉率的變化關系,其中下陷量和掛鉤牽引力值取各工況穩定狀態下的均值。由圖可知:輪胎的下陷量隨滑轉率的增加而逐漸增加,而且其增加趨勢逐漸“陡峭”,該趨勢與文獻[17]研究結果基本一致。
掛鉤牽引力隨滑轉率的增加逐漸增加,當滑轉率小于25%時,增加趨勢較陡峭,當滑轉率大于25%時,增加趨勢緩慢,該現象也與文獻[17]實驗結果整體趨勢一致。
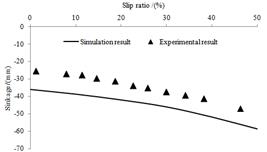
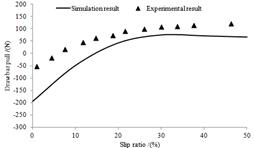
圖12 輪胎下陷量隨滑轉率變化關系 圖13 掛鉤牽引力隨滑轉率變化關系
4 結 論
將FEM/DEM方法應用于車輪在沙石路面的行駛行為仿真分析,并提出了一種“路面更替法”。路面更替法可以實現一定數量的離散單元來模擬任意長度的沙石路面,達到控制模型規模,提高計算效率的目的。
輪胎行駛行為,包括路面豎直方向反作用力,掛鉤牽引力,下陷量及輪胎行駛過程中沙石顆粒的流動狀況等都可很方便地通過計算求得,數值試驗結果與實驗結果對比驗證了該方法的有效性。
參考文獻
[1] Xia K. Finite element modeling of tire/terrain interaction: Application to predicting soil compaction and tire mobility[J]. Journal of Terramechanics. 2011;48:113-23.
[2] Xia K, Yang YM. Three-dimensional finite element modeling of tire/ground interaction[J]. International Journal For Numerical and Analytical Methods in Geomechanics. 2012;36:498-516.
[3] Li H, Schindler C. Analysis of soil compaction and tire mobility with finite element method[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics. 2013;227:275-91.
[4] González Cueto O, Iglesias Coronel CE, Recarey Morfa CA, Urriolagoitia Sosa G, Hernández Gómez LH, Urriolagoitia Calderón G, et al. Three dimensional finite element model of soil compaction caused by agricultural tire traffic[J]. Computers and Electronics in Agriculture. 2013;99:146-52.
[5] Li H, Schindler C. Three-dimensional finite element and analytical modelling of tyre–soil interaction[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics. 2013;227:42-60.
[6] Smith W, Peng H. Modeling of wheel-soil interaction over rough terrain using the discrete element method[J]. Journal of Terramechanics. 2013;50:277-87.
[7] Li W, Huang Y, Cui Y, Dong S, Wang J. Trafficability analysis of lunar mare terrain by means of the discrete element method for wheeled rover locomotion[J]. Journal of Terramechanics. 2010;47:161-72.
[8] 張銳, 劉芳, 曾桂銀, 李建橋. 非規則車輪 散體模擬月壤相互作用仿真系統研究[C]. 顆粒材料計算力學研究進展2012.
[9] Jiang M, Liu F, Shen Z, Zheng M. Distinct element simulation of lugged wheel performance under extraterrestrial environmental effects[J]. Acta Astronautica. 2014;99:37-51.
[10] Nakashima H, Takatsu Y, Shinone H. Analysis of tire tractive performance on deformable terrain by finite element-discrete element method[J]. Journal of Computational Science and Technology. 2008;4:423-34.
[11] Nakashima H, Takatsu Y, Shinone H. FE-DEM analysis of the effect of tread pattern on the tractive performance of tires operating on sand[J]. Journal of Mechanical Systems for Transportation and Logistics. 2009;2:55-65.
[12] Nakashima H, Oida A. Algorithm and implementation of soil-tire contact analysis code based on dynamic FE-DE method[J]. Journal of Terramechanics. 2004;41:127-37.
[13] Williams J, Perkins E, Cook B. A contact algorithm for partitioning N arbitrary sized objects[J]. Engineering Computations. 2004;21:235-48.
[14] Zang MY, Gao W, Lei Z. A contact algorithm for 3D discrete and finite element contact problems based on penalty function method[J]. Computational Mechanics. 2011;48:541-50.
[15] Balevi?ius R, D?iugys A, Ka?ianauskas R. Discrete element method and its application to the analysis of penetration into granular media[J]. Journal of Civil Engineering and Management. 2004;1:3-14.
[16] Han K, Peric D, Crook A, Owen D. A combined finite/discrete element simulation of shot peening processes–Part I: studies on 2D interaction laws[J]. Engineering Computations. 2000;17:593-620.
[17] Shinone H, Nakashima H, Takatsu Y. Experimental analysis of tread pattern effects on tire tractive performance on sand using an indoor traction measurement system with forced-slip mechanism[J]. Engineering in Agriculture, Environment and Food. 2010;3:61-6.
[18] Zang M, Zhao C. Numerical Simulation of Rigid Wheel Running Behavior on Sand Terrain[C]. 2013.
[19] 莊繼德. 計算汽車地面力學[M]: 機械工業出版社; 2002.
